How to Draw a Circle From an Equation
Circle Equations

A circumvolve is easy to make:
Draw a curve that is "radius" away
from a primal point.
Then:
All points are the same altitude
from the center.
In fact the definition of a circle is
Circle: The set up of all points on a plane that are a fixed distance from a eye.
Circle on a Graph
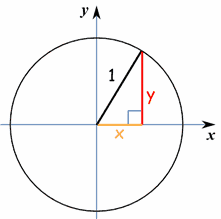
Permit us put a circle of radius five on a graph:

Now let's work out exactly where all the points are.
We make a correct-angled triangle:

And and so use Pythagoras:
102 + y2 = 52
There are an space number of those points, here are some examples:

| x | y | x2 + y2 |
|---|---|---|
| 5 | 0 | 5two + 02 = 25 + 0 = 25 |
| three | 4 | 3ii + ivii = 9 + sixteen = 25 |
| 0 | 5 | 02 + 5ii = 0 + 25 = 25 |
| −four | −iii | (−4)2 + (−3)2 = 16 + 9 = 25 |
| 0 | −five | 0ii + (−5)2 = 0 + 25 = 25 |
In all cases a point on the circle follows the rule xii + y2 = radiusii
We can use that idea to find a missing value
Instance: x value of ii, and a radius of five
Commencement with: x2 + y2 = r2
Values we know: ii2 + y2 = 52
Rearrange: ytwo = 5ii − two2
Foursquare root both sides: y = ±√(52 − 22)
Solve: y = ±√21
y ≈ ±iv.58...
(The ± means there are ii possible values: one with + the other with −)
And here are the two points:

More General Case
Now let us put the centre at (a,b)

So the circle is all the points (x,y) that are "r" abroad from the center (a,b).
At present lets piece of work out where the points are (using a right-angled triangle and Pythagoras):

Information technology is the aforementioned idea equally earlier, but we need to subtract a and b:
(x−a)2 + (y−b)2 = rii
And that is the "Standard Form" for the equation of a circumvolve!
It shows all the important information at a glance: the center (a,b) and the radius r.
Example: A circle with center at (3,iv) and a radius of six:
Showtime with:
(x−a)two + (y−b)2 = r2
Put in (a,b) and r:
(ten−3)2 + (y−4)two = 62
We can then apply our algebra skills to simplify and rearrange that equation, depending on what we need information technology for.
Try information technology Yourself
images/circumvolve-equn.js
"Full general Form"
But y'all may encounter a circumvolve equation and not know it!
Because it may not be in the bang-up "Standard Form" to a higher place.
As an example, let us put some values to a, b and r and then aggrandize it
Start with: (x−a)2 + (y−b)two = r2
Case: a=1, b=ii, r=3: (10−1)two + (y−2)2 = iii2
Expand: x2 − 2x + 1 + ytwo − 4y + 4 = 9
Gather similar terms: xii + y2 − 2x − 4y + 1 + 4 − 9 = 0
And nosotros end upwards with this:
x2 + ytwo − 2x − 4y − iv = 0
Information technology is a circle equation, but "in disguise"!
So when you see something similar that recollect "hmm ... that might be a circle!"
In fact we can write it in "Full general Form" by putting constants instead of the numbers:
x2 + yii + Ax + By + C = 0
Note: General Form always has x2 + y2 for the first 2 terms.
Going From General Form to Standard Form
At present imagine we take an equation in Full general Class:
x2 + y2 + Ax + By + C = 0
How tin we go it into Standard Grade similar this?
(x−a)2 + (y−b)ii = r2
The respond is to Complete the Foursquare (read about that) twice ... once for ten and once for y:
Case: 10two + y2 − 2x − 4y − four = 0
Showtime with: x2 + y2 − 2x − 4y − 4 = 0
Put xs and ysouth together: (tenii − 2x) + (y2 − 4y) − four = 0
Constant on right: (xtwo − 2x) + (y2 − 4y) = 4
At present complete the foursquare for x (have half of the −2, square it, and add together to both sides):
(ten2 − 2x + (−one)two ) + (y2 − 4y) = iv + (−one)2
And complete the square for y (take half of the −iv, square it, and add to both sides):
(xii − 2x + (−1)2) + (y2 − 4y + (−2)2 ) = 4 + (−one)2 + (−two)ii
Tidy up:
Simplify: (x2 − 2x + 1) + (y2 − 4y + 4) = ix
Finally: (10 − 1)ii + (y − 2)ii = 3two
And we have it in Standard Form!
(Note: this used the a=ane, b=ii, r=three example from before, so we got information technology right!)
Unit Circumvolve
If we identify the circumvolve center at (0,0) and gear up the radius to 1 we get:
 | (10−a)2 + (y−b)ii = rtwo (x−0)2 + (y−0)ii = ane2 x2 + y2 = ane Which is the equation of the Unit Circle |
How to Plot a Circumvolve by Hand
ane. Plot the centre (a,b)
two. Plot four points "radius" away from the center in the upwardly, downwardly, left and right management
3. Sketch it in!
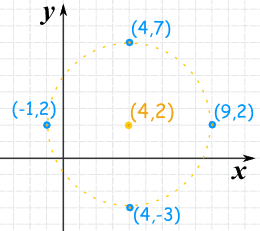
Example: Plot (ten−4)ii + (y−ii)2 = 25
The formula for a circle is (x−a)2 + (y−b)2 = r2
So the center is at (4,2)
And r2 is 25, so the radius is √25 = 5
Then we can plot:
- The Heart: (4,2)
- Upward: (4,2+5) = (iv,7)
- Down: (4,2−5) = (4,−3)
- Left: (4−five,2) = (−1,2)
- Right: (four+v,two) = (9,2)
Now, just sketch in the circle the best we tin can!
How to Plot a Circumvolve on the Estimator
Nosotros need to rearrange the formula and so we get "y=".
We should finish up with two equations (acme and lesser of circumvolve) that tin can and so be plotted.
Example: Plot (x−4)2 + (y−2)2 = 25
Then the center is at (four,2), and the radius is √25 = 5
Rearrange to go "y=":
Offset with: (x−4)two + (y−2)2 = 25
Move (10−4)ii to the correct: (y−2)ii = 25 − (10−4)2
Take the square root: (y−2) = ± √[25 − (ten−4)2]
(notice the ± "plus/minus" ...
at that place can be 2 square roots!)
Motility the "−2" to the right: y = 2 ± √[25 − (x−four)2]
So when we plot these two equations we should have a circle:
- y = 2 + √[25 − (x−iv)ii]
- y = 2 − √[25 − (x−4)ii]
Try plotting those functions on the Part Grapher.
It is besides possible to use the Equation Grapher to do it all in one go.
8526, 8527, 8539, 8540, 8515, 8516, 569, 8544, 8559, 8560, 570, 1209
Source: https://www.mathsisfun.com/algebra/circle-equations.html
0 Response to "How to Draw a Circle From an Equation"
Postar um comentário